Margins of success in fixed-die systems

Previously, we looked at effective hit points in fixed-die systems with binary hit/miss outcomes. Of course, this isn’t the only possible outcome structure. It’s common for systems to have some sort of critical hit mechanic, effectively introducing a third possible outcome. Some systems may go as far as using the full margin of success (MoS) –the difference between the player’s result and the target number –to determine the magnitude of the success.

For this article, we’ll assume the margin of success is one-sided; in other words, there are no margins of failure; or in yet other words that failure merely results in zero value for the player and not negative value.

Intuition

Before diving into the mathematics, we should think about what we might expect from switching from a binary hit/miss system to a margin of success system. We can think of the possible results of a die roll as a “window” (e.g. 1 to 20 on a d20) that slides over a range of possible outcomes depending on the modifier that’s added to it.

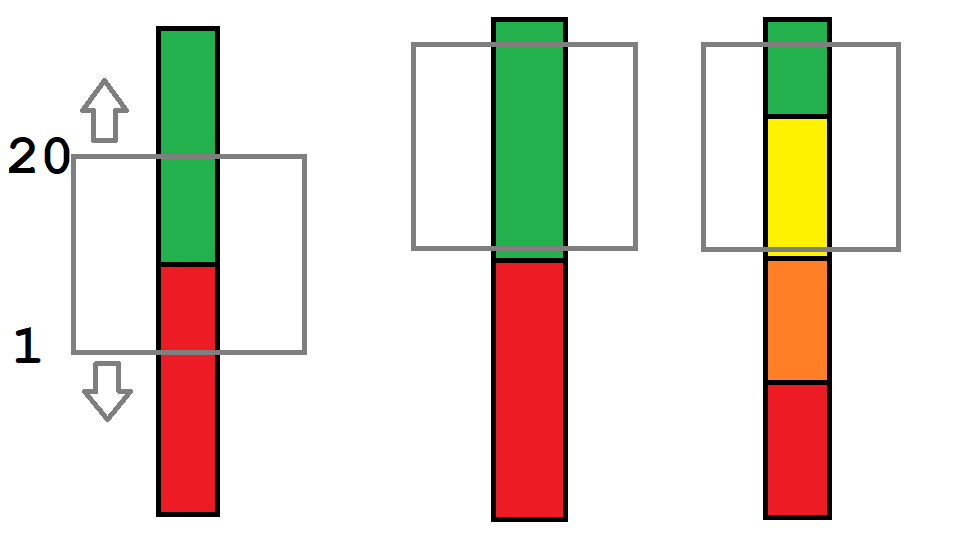
If there are only two possible outcomes (left), then the modifier stops making a difference once the window slides so far in either direction that the threshold between them is no longer in the window (center). On the other hand, if there are more than two possible outcomes, then modifiers continue to matter as long as at least one of the thresholds is inside the window (right). Therefore, we can expect the following when we switch from a binary system to a margin of success system:

• The MoS system will have a wider useful range where modifiers continue to make a difference.
• If we are typically near the center of the useful range but only the worst result is considered a miss, the typical hit chance will increase.

Mean damage

While the above applies to both quantifiable and non-quantifiable outcomes, we’re going to see how this intuition works out mathematically. If you’re not too concerned with the math details, you can skip to the conclusion.

We’ll use mean damage as our metric: damage is a common mechanic and it has a clear quantifiable value. We’ll say that damage is directly proportional to MoS + 1 (counting ties as hits for 1 damage). This isn’t the only possible MoS system, nor necessarily even a good system for a particular application; we are just using this to illustrate general patterns of what we can expect from a MoS outcome system compared to a binary hit/miss system.

Margins of success presents an additional complication: unlike binary hit/miss, the mean damage of a hit is not constant. In order to be able to compare them, we’ll assign a damage value to the binary system. We’ll choose whatever damage values line up our curves the best.

Although we’ll frame things as attack bonus versus AC, this can also apply to other situations such as armor that reduces damage from hits by a flat number. In that case, having all of the attack’s damage blocked is analogous to a “miss”.

Plotting

In our previous series, we plotted effective hit points (EHP) versus the number needed to hit. This is because our main concern was the rapid increase in EHP on the right side of the graph (high to-hit numbers, low chance to hit), and the EHP graph shows this better.

However, this time we will be more concerned with the left side of the graph (low to-hit numbers, high chances to hit), namely the increase in mean damage there, or lack thereof. As such, we will plot mean damage rather than EHP. Remember that EHP and mean damage are reciprocals of each other.

Standard dice

The obvious thing to do when considering switching from a binary system to a MoS system is to keep exactly the same dice and modifiers. However, this doesn’t work very well as a drop-in replacement. Here’s what happens when we do this on a standard d12.

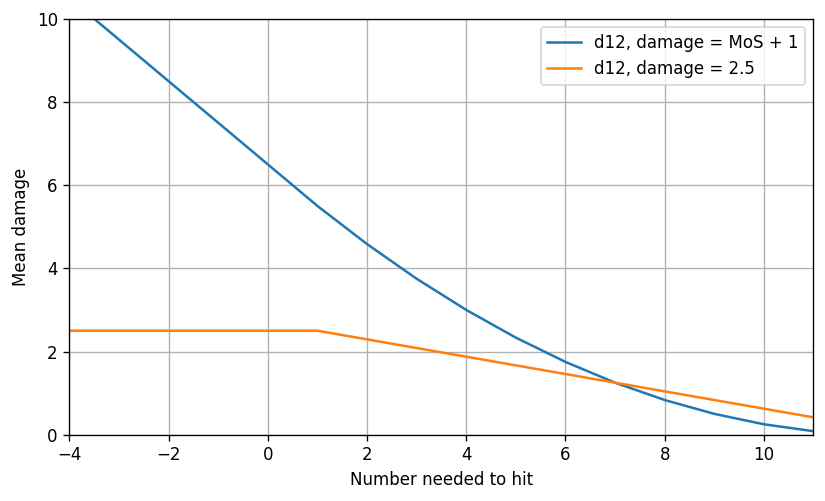
Or, on a logarithmic vertical axis:

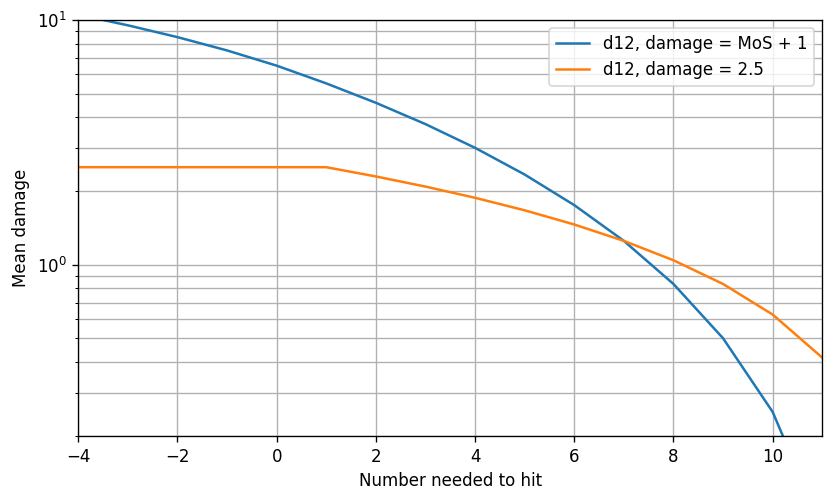
Here we’ve chosen the damage for the binary system so both systems have similar mean damage at the 50th percentile. The slope for the MoS system is considerably steeper than the slope for the binary system, meaning that this change increases the value of modifiers near the 50th percentile, or equivalently, reduces the granularity of modifiers.

(There’s nothing special about the 50th percentile here; we’re just using 50% as an example typical hit chance. We could just as easily have used 60% or some other percentile as our typical hit chance.)

The logarithmic vertical axis makes it easier to match curves since it makes scaling of damage simply move the curve up and down without any stretching. Also note that on a logarithmic vertical axis, the EHP plot is simply the mean damage plot flipped upside-down.

Matching the 50th percentile

A better comparison is to once again match the 50th percentiles, as we did previously. One way to do this is to increase the die size when we switch to the MoS system, thus making the slopes match on the logarithmic scale. Another way of looking at it is that we can use a larger die size to make up for the lost granularity. For now, we’ll maintain the same typical hit chance. For standard dice, usually a factor of between 1.5× to 2× die size when switching from binary to MoS will match the slopes around the 50th percentile.

For example, here’s the same graph, except we increased the MoS die to a d20 and rescaled the damage, matching a 50% hit chance in the binary system to 50% hit chance in the MoS system.

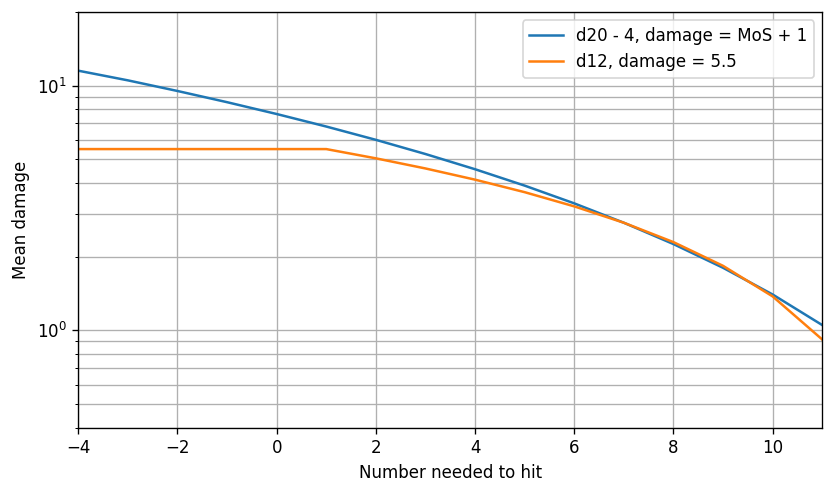
Now we can make a better comparison, since the two curves are close to each other near the 50th percentile. The MoS system has a longer left tail, because hit chances above 100% continue to add extra damage with MoS, whereas with binary hit/miss they stop doing anything.

Sum of multiple standard dice

What about the sum of multiple standard dice? The result is similar:

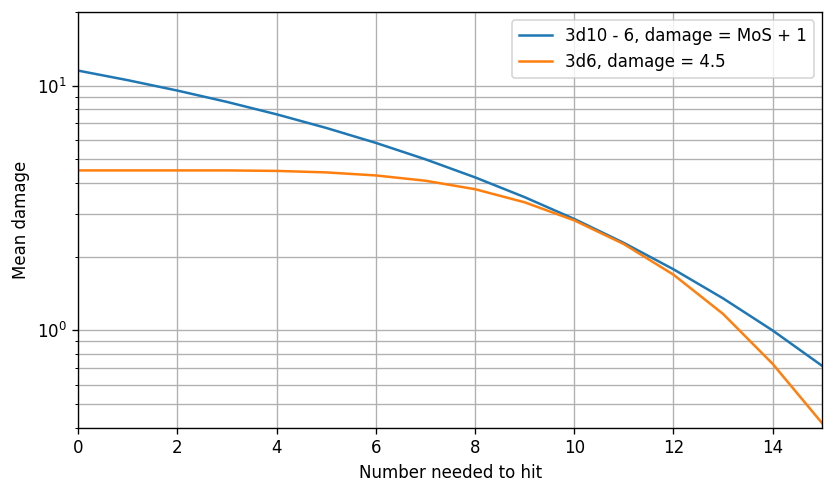
Since any opposed system with standard dice can be transformed into one where one side rolls all the dice, this applies to opposed systems as well.

Shifting the typical hit chance

Instead of increasing the die size, which lowers the slope of the curve everywhere, we could increase the typical hit chance, i.e. increasing the typical attack bonus relative to AC. This shifts the curve right, thus using a region of the curve with a shallower slope on the logarithmic plot. This can be tuned so that we again achieve the same slope around the typical hit chance.

A higher typical hit chance works better in a MoS system compared to a binary system because it has the left tail to work with. Increasing the typical hit chance effectively replaces near-misses with weak hits.

For example, in our 3d6 example, instead of changing the dice to 3d10, we can add 3:

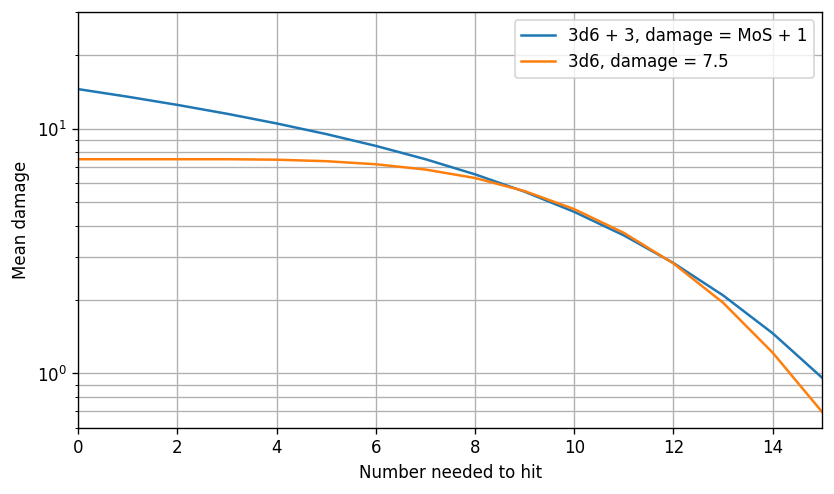
In this case, the typical hit chance increased from half to about 5/6. This still works fine for the MoS system, since additional points of attack bonus will contribute extra damage even if the hit chance is already near or at 100%. In contrast, if we give a binary system a typical hit chance of 5/6, additional points of attack bonus soon stop having much or any effect.

Here are the last three curves on a linear vertical axis:

Geometric dice

What about geometric dice? Well, it turns out that for an ideal geometric distribution, the mean damage of a hit (conditional on hitting) doesn’t change at all below 100% hit chance when we switch to a MoS system. In fact, the entire probability distribution of damage here (again, conditional on hitting) doesn’t change: the damage on a hit is equal to rolling the geometric die with no modifier.

What does change is that damage continues to increase past 100% hit chance as they did with standard dice, and any bumps caused by using a standard exploding die rather than an ideal geometric die are smoothed out somewhat:

Here we’ve intentionally separated the two pairs of curves by a factor of 4 in damage to make them easier to see.

Opposed exploding dice are similar:

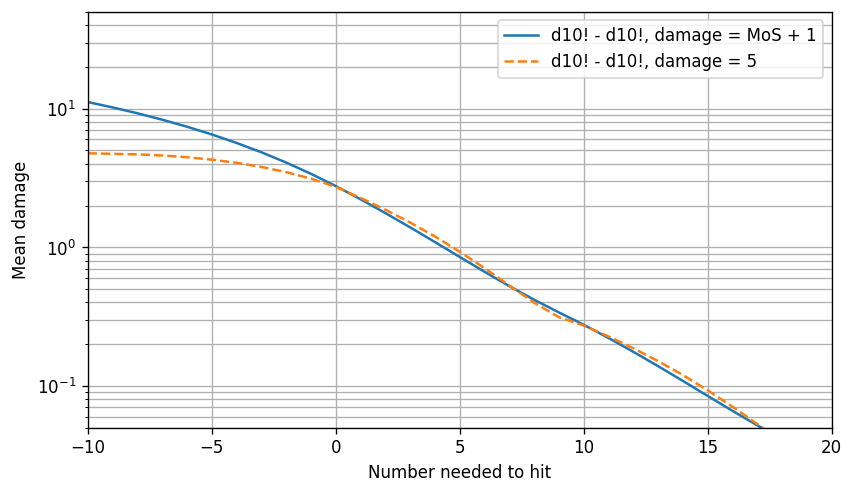
Observe that the left tail caused by the MoS system is more significant than that of adding standard dice to exploding dice or doing an opposed roll. This is because hit chances cap out at 100% but MoS doesn’t cap.

Other margin of success effects

So far we had damage increase linearly with the margin of success. Here are a couple other options.

Capped margin of success

If we put a maximum limit on the margin of success, then the left tail will stop after a while. This tends to make the behavior somewhere between binary systems and the uncapped MoS systems we’ve been looking at so far. For example, here’s a comparison of a Pathfinder-2e-like¹ system (beating the AC by 10 results in double damage) with a binary system and a linear MoS system with similar behavior around the 50th percentile:

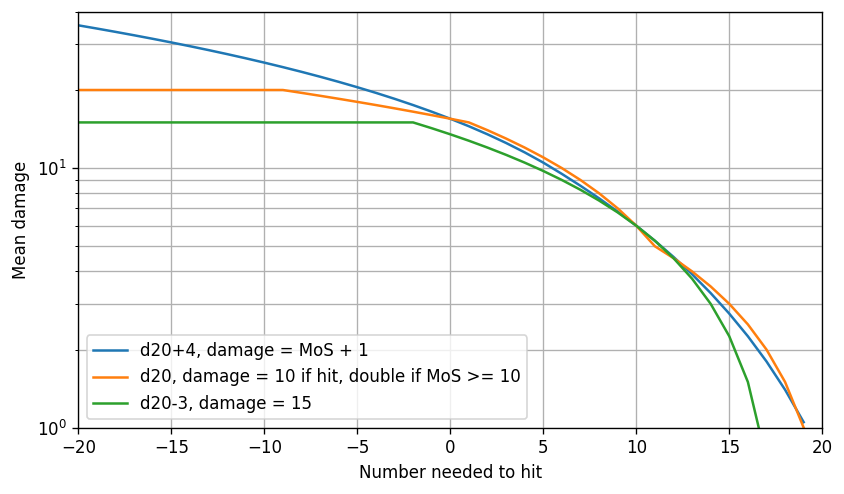
The tail does eventually flatten out like a binary system and unlike an uncapped MoS system, but it doesn’t flatten out as quickly as the binary system.

Multi-tier critical hits

In the opposite direction, instead of linearly scaling damage with margin of success, we could double the damage for every X points above the MoS, effectively introducing multiple tiers of critical hits. Each additional point of modifier beyond 100% hit chance then increases the damage by about a constant proportion rather than a constant absolute amount.

For example, we could double the damage for beating the AC by 5, double it again to 4× damage at 10, again to 8× at 15, and so forth. Here’s an example with 3d6:

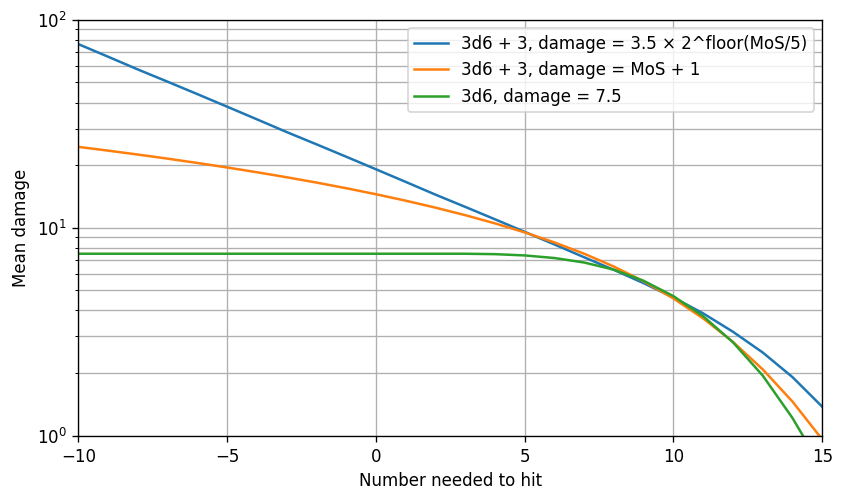
Note that this example doesn’t have the sharp corners of the Pathfinder-2e-like curve. This is because the bell-shaped curve of 3d6 gradually introduces each tier of critical hits, unlike the uniform distribution.

With a linear vertical axis:

This type of system allows attackers with a high advantage to hit like gods, which may be appropriate for certain styles of games.

We must take extra care if we use this with geometric or exploding dice, however. The doubling of damage must be slower than the half-life of the dice or else the mean damage becomes infinite! Another way of putting it is: as we double the damage faster, the share of all damage done by normal hits decreases and the share of all damage done by critical hits increases. We can prevent this by making it take longer than a half-life to double the damage; for example, if the geometric dice have a half-life of 3, we could double the damage every 5 or every 10 points of margin of success.

Conclusion

This concludes our mathematical analysis of the mean damage of MoS. If we hold behavior near the 50th percentile (or most plausible typical hit chances) constant, the major mathematical effects of switching from a binary hit/miss system to a MoS system are:

• Modifiers continue to make a difference up to and beyond 100% hit chance. This can extend the useful region of the curve, especially if typical hit chances are increased to use more of the left tail.
• For standard dice, in order to maintain similar behavior around typical hit chances when switching from binary to MoS, either the die size should increase, or typical hit chances should increase. Since smaller numbers are easier to add, this is another reason why MoS works best when combined with increased typical hit chances.
• MoS smooths out bumps in damage curves a bit, such as those caused by exploding dice.

However, we must also weigh other aspects that don’t directly deal with mean damage, which if anything are even more important. Here are some of these aspects to consider when deciding whether to use a MoS system rather than a binary system:

• Most importantly, MoS adds complexity. It’s another rule to remember and process, and subtraction isn’t the easiest operation for humans. A middle ground is to only use a small number of easy-to-remember thresholds (e.g. the Pathfinder 2e system) rather than a full subtraction. This is especially easy in systems with fixed target numbers such as PbtA-type games. Roll-under systems can use the “price is right” method.
• MoS could potentially take the place of e.g. damage rolls, thus trading increased complexity in one area for decreased complexity in another. However, this sacrifices the flexibility of decoupling damage from attack rolls.
• The mathematical advantages of MoS are in its behavior at high hit chances — even beyond 100% hit chance. If you like high hit chances, this may be a good thing; on the other hand, if you hate guaranteed hits, that may be a reason not to use MoS. Or use a mechanic that always gives a chance to miss, such as “natural 1s always miss” or opposed exploding dice.
• MoS naturally produces multiple possible outcomes, which can add interest to each roll. This is especially true with exploding dice, where there’s always a chance (however tiny) of getting an amazing result. Note however that MoS isn’t strictly necessary to produce multiple possible outcomes: with rolls of a binary hit/miss system, we can produce up to outcomes by counting hits/successes. (Or up to by branching, though this can get very complicated very quickly.)
• It’s easy to create multiple levels of outcomes with damage: just make higher margins of success deal more damage. It’s more difficult for other types of rolls, but potentially also more rewarding. Even for non-numerical outcomes, MoS expands the part of the curve where modifiers continue to make a difference.

---

¹ Here we are only considering the “beat AC by 10 to crit” rule. This isn’t the entire Pathfinder 2e critical system; we are not considering the rules about natural 20s and 1s, the possibility for extra special effects on critical hits, critical failures, and so forth. This is primarily an example rather than a statement on Pathfinder in particular.